How Can I Create My Favorite State Ranking?
By The Economic Development Curmudgeon
 How Can I Create My Favorite State Ranking: The Hidden Pitfalls of Statistical Indexes
How Can I Create My Favorite State Ranking: The Hidden Pitfalls of Statistical Indexes
Yasuyuki Motoyama, Ph.D.
Jared Konczal
Ewing Marion Kauffman Foundation
The authors would like acknowledge Dane Stangler, Arnobio Morelix, Michelle St. Clair, Lacey Graverson, Melody Dellinger and Kate Maxwell
State economic rankings are both pervasive and popular. The long list of well-known rankings includes the State Competitiveness Report by the Beacon Hill Institute, the State New Economy Index by the Information Technology and Innovation Foundation,[1] the Cost-of-Doing-Business Index by the Milken Institute, the Economic Freedom Index by the Pacific Research Institute, and the State Business Tax Climate Index by the Tax Foundation, among many others. These rankings–and even many that are less familiar–receive substantial media attention on the scale of thousands of viewers each day. As a result, media outlets have started to create their own rankings: Forbes’ Best States for Business and CNBC’s America’s Top States for Business. We know that there are more than one dozen out there, and the list seems to grow every year. [1]
[[1] Disclosure: the Kauffman Foundation has given grant funding to support this report in the past. Also, Kauffman research has been used as the basis for ranking states, most notably on the rate of entrepreneurial activity, formalized in the Kauffman Index of Entrepreneurial Activity. This is an index-based data from the U.S. Census Bureau and Bureau of Labor Statistics, and has never been a normative attempt to claim that one state or another is “better” for entrepreneurs.]
So business climate indexes have become a cottage industry within the economic development profession. Reacting to, and explaining why and how their state-community is ranked by business climate indexes has accordingly become a cottage industry among state and sub-state economic developers. The combination of publishing indexes and states and community’s reacting to them has not been a pretty picture–in fact, it can be quite challenging and sometimes demeaning.
Frankly, a serious measure of cynicism, opportunism, confusion, and manipulation has also entered this dismal business climate index picture. A large part of the business climate index “problem” is that, at heart, business climate indexes are a statistical and methodological concoction drawn from a database that is unavailable to the economic developer, the media, or the governance of your agency-community. We, as state and sub-state economic developers, are pretty much at the mercy of the entity and researcher compiling and presenting the index. Understanding statistical findings derived from poorly explained methodologies is usually not the forte of a state and sub-state economic developer. Hence this article. Statistics and methodologies are a magical land that badly needs some explanation.
What You Should Know About the Methodology and Statistics of Indexes
Despite their popularity and seemingly daunting sophistication, these rankings come with major limitations. First, it is not clear what exactly each ranking is measuring, and if they accurately assess what they claim to measure. This criticism may not apply to the simplest rankings; for example, the Tax Climate Index scores states only by their tax rates. If you assume that lower tax rates in any form (personal, corporate, sales, and property) are uniformly better for operating businesses, this ranking offers accurate information.
Other rankings, however, may have significant internal validity problems. For instance, the Small Business and Entrepreneurship Council’s Small Business Survival Index purportedly measures “major government-imposed or government-related costs affecting investment, entrepreneurship, and business” (SBEC, 2011, p. 5). They employ twenty-three indicators to create the index, including the state’s taxes, right-to-work status, minimum wage level (relative to the federal level), health care and electricity costs, crime rate, and number of government employees. While it is easy to measure these costs of government, this system fails to factor in the benefits generated by government, such as investment in infrastructure, education systems, small business development centers, and business extension services.
As the number of factors or variables on which the rankings are constructed becomes more numerous, the validity problem becomes even more pronounced. The Pacific Research Institute’s Economic Freedom Index, for example, claims to measure free enterprise and consumer choice. One component of the index is a judicial score that is based on a creative combination of 1) straightforward quantifiable indicators, such as the compensation and terms of judges and the number of active attorneys (though it is not clear if higher judicial compensation is better or worse for the state–assumptions creep in almost without our realizing it), and 2) qualitative indicators, such as whether the state has had liability reform, class action reform, and jury service reform. Unfortunately, they do not provide a breakdown or discussion of the method for compiling these measures. And while the Pacific Research Institute admits that “it is not easy to interpret these indicators” (PRI 2008, 26), this judicial score is one of the five major components of its index. Perhaps, the methods have become so complex that the rankings’ creators themselves can feel a bit wary.
The second limitation of these rankings is that research has found few correlations between rankings and actual economic growth-related indicators at the state level. Fisher (2005) tried hard to find connections by examining firm formation rate, job creation by the state economy, jobs created by fast-growing Inc. firms, the number of initial public offerings, and issued patents. None of the eight rankings he examined had statistically significant relationships to these indicators. Steinness (1984) and Skoro (1988) came to the same conclusion. Plaut and Pluta (1983) and Kolko et al. (2011) conducted more sophisticated, multivariate analyses, but had no luck, either. The rankings we have mentioned thus far are created by consultants and think tanks with specific ideologies.
Do academic rankings provide any insights? While we do not find academic rankings of state business per se, there has been work on some metropolitan rankings. Chapple et al. (2004) ranked high-tech areas based on occupational data instead of traditional industry-based data, and Gottlieb (2004) created the Metropolitan New Economy Index. However, Cortright and Mayer (2004) cautioned that rankings, as they are often based on a uni-dimensional scale, almost inevitably are vastly too simple to measure a complex, multi-faceted phenomenon such as job creation, business formation or innovation. Also as claimed by Gottlieb (2004), each individual ranking may have a different purpose and use different measures. Comparability between rankings is almost impossible, so academic debates about rankings do not seem to offer us any solution.
An even worse problem is the effect these indexes exert on state and local economic developers. The current abundance of methodologically fragile rankings leads to misuse of them at the policy level. Abuse can be observed primarily in two ways. In one case, policymakers choose a conveniently positive ranking for their state and celebrate their performance (or political-ideological opponents use them to attack). In another case, state government officials or economic development consultants choose rankings in which a state performs poorly to instigate efforts to remedy that problem, and justify a reform action or a sales pitch.
Can a Business Climate Index usefully measure a real-life business climate?
Frankly, we reject the argument that because it purports to measure a very specific aspect of the state or metropolitan economy, a business climate index-ranking is helpful to economic development. Unless the researcher can truly identify and use a specific output indicator or measurement which mirrors the factor (job creation, business formation or innovation, for instance) the ranking, bluntly, is meaningless.
Moreover, our forthcoming research (Motoyama and Hui,2014) demonstrates that many rankings do not even correlate with business owners’ business climate perceptions. Without any connection to macroeconomic indicators or perceptions of business owners, the primary target of rankings, what validity can these indexes and their rankings possess? We will demonstrate in the sections below that the limitations of every methodology, given the complexity of what they seek to measure (innovation, business formation or job creation, for instance), can easily–sometimes unconsciously, sometimes consciously–result in misleading or “manipulated” rankings. Even with good data and sound, transparent methodology, the process of creating rankings is extremely subjective.
Subjectivity is a Relative Matter
In the remainder of this article, we conduct a series of hypothetical decisions that any researcher constructing a business climate index could likely encounter/make and then demonstrate how unintentionally or not these simple decisions can lead to significant fluctuations in the index rankings. These decision points are seldom acknowledged in the index and are often unknown to consumers. The numbers may reflect the state-level data, but they do not necessarily mean what the reader and consumer of the index think they mean, and thus we show how easily the rankings can be manipulated or misused.
Next, we will employ Pearson correlation analysis to demonstrate to the reader which indicators are correlated with innovations and entrepreneurship. [For statistical geeks who demand even more sophisticated methodology we will, at the end of this article provide a principal components analysis.] Finally in the last section, we will “play around with” or simulate these statistics to show how easy it is to affect the state rankings by making different, perfectly reasonable, research decisions and using different assumptions. Each decision will lead to creating personal rankings from various combinations of the measures. Maybe statistics really can lie? Here’s how business indexes are ever so easily subjective and usually misleading. [
[Reader please understand that it is not necessary to follow the statistical methodology–feel free to leave that to the geeks in the crowd. What you should do is see how one can start out with seemingly fine indicators, then employ appropriate and sound statistical operations, and wind up with clusters of states that make no theoretical or apparent sense. Then, in the search for some meaning, the researcher “plays around with” some of the indicators, adjusts the statistics in some fashion (watch out for us throwing out the outliers for instance), and then comes up with new rankings. While a good magician should never disclose how his tricks work, a good researcher ought to believe that an educated consumer is preferable to a deceived or confused one]
We must consider some indicators to compare. First, we select three reasonable, even commonsensical, indicators to measure levels of entrepreneurship in any state:
- 1) The self-employment rate, cross-tabulated from the Public Use Micro Sample of the American Community Survey. This self-employment measure captures a wide range of entrepreneurial activity because it includes everything from mom and pop shop owners and independent consultants to owners of large firms;
- 2) The Kauffman Index of Entrepreneurial Activity, which uses the Current Population Survey (CPS) to measure any form of business creation, with or without employment, in the previous twelve months;
- 3) Start-up rate from the Business Dynamics Statistics (BDS) data series. We calculate the ratio of the number of firms that are fewer than five years old to the total number of firms. We focus on this threshold because Haltiwanger and his colleagues (2012, 2013) have demonstrated that much of the new employment in this country has been created by firms five years old or younger.
Second, in order to measure levels of innovations, we rely on data provided primarily by the National Science Foundation’s Science and Engineering Indicators. We use the following indicators:
- 4) Science &Engineer: The ratio of science and engineering bachelor degree holders to the total population;
- 5) Patents: Patents per science and engineering workforce;
- 6) VC: Venture capital investment over Gross State Product (GSP);
- 7) R&D: Research and development expenditure by industry and university over GSP; and
- 8) Inc.: The number of high-growth Inc. 500 firms, using data from Inc. Magazine, normalized by population per million.
Finally, we use per capita Gross State Product (GSP) as our benchmark, or proxy for change in state economic development performance. [Note that all indicators are normalized by population (i.e. per capita); without normalization, any correlation would be biased by the varying population of each state. and they are presented as a ratio, with population as the denominator]. While most of these indicators below are considered reliable and are from good data sources, some indicators experience fluctuations during the three-year observation period, so we calculated an average of the values between 2008 and 2010. In this way, we can capture more smooth and stable correlations between indicators. [Doesn’t it seem perfectly reasonable to have “smooth and stable correlations”?] Table 1 summarizes.
Table 1: Explanation of Variables
|
# |
Name |
Description |
Source |
Year(s) |
| Entrepreneurship Variable | ||||
| 1) | Self-employment | Self-employed individuals as a fraction of the total population | American Community Survey | 2008-10 |
| 2) | Kauffman Index of Entrepreneurial Activity | Adults starting a business (employer and non-employer) in the last year as a fraction of all adults | Current Population Survey | 2008-10 |
| 3) | Business Dynamics Statistics (BDS) | Firms ages five or younger, as a fraction of all firms | Business Dynamics Statistics | 2008-10 |
| Innovation Variable | ||||
| 4) | Scientists & Engineer (Science &Engineering) | Science & engineering bachelors holders as a fraction of the total population | Science & Engineering Indicators | 2008-10 |
| 5) | Patents | Patents per science and engineering workforce | Science & Engineering Indicators | 2008-10 |
| 6) | Venture Capital (VC) | Venture capital investment per GSP | Science & Engineering Indicators | 2008-10 |
| 7) | Research & Development (R&D) | Industry and university R&D over GSP | Science & Engineering Indicators | 2007,08 |
| 8) | Inc. firms | Inc. 500 firms per million population | Inc. Magazine | 2008-10 |
| Reference Variable | ||||
| 9) | GSP per capita | Gross State Product per capita | Survey of Current Business, Bureau of Economic Analysis |
2010 |
Logically, we begin our analysis with all 50 states and the District of Columbia. As correlations can be easily biased by outliers, we first identify outliers by plotting histograms. Highly-skewed distributions on the tails of the right side indicate that there are outliers in Science &Engineer, patents, VC, Inc., and GSP per capita. For VC, the two outliers are California and Massachusetts, as we would expect in the two states that have a high concentration of venture capital firms. In all other cases, the outlier is DC. As a result, we omit DC from the rest of our analysis [bye, bye DC; why didn’t we throw out outliers California and Massachusetts? Throwing out the ground zero of innovation and venture capital would make no sense].
Chart 1: Histogram of investigated indicators (Left Click to Enlarge)
Next we apply Pearson Correlation Analysis We now conduct analysis using Pearson correlations as our measure. Logically, it would seem reasonable to assume that all our correlations for entrepreneurship (the three indicators in the table above) and the five indicators for innovation should be high. One would also expect that correlations between entrepreneurship and innovation be high. Are these assumptions reasonable–are the indicators correlated with each other? Are innovation and entrepreneurship correlated with each other? If they are not highly correlated, why aren’t they? Are they bad indicators?
[For the reader a good reference point for the below correlations of about 0.4 means is that each of these indicators can explain only about 40 percent of variation to each other, which we consider low for data supposedly measuring the same theme. 60% of our understanding of what is going on is missing. Maybe it would be better to toss a coin?] Rather surprisingly, when we apply Pearson correlations, we find that many indicators are only modestly correlated or not correlated at all.
Rather surprisingly, when we apply Pearson correlations, we find that many indicators are only modestly correlated or not correlated at all.
Furthermore, even within a set of indicators, the indicators have little correlation. For example, self-employment is modestly correlated (0.655) with Business Dynamic Statistics, but does not correlate to the Kauffman Index. Within innovation indicators, the best correlations are VC and Inc. (0.472), VC and Science &Engineering (0.443), Science &Engineering and patents (0.420), and patents and VC (0.399). One mysterious finding is the high correlation between self-employment and R&D. For some reason, 99.8 percent of changes in self-employment can be explained by R&D, and vice versa. We do not yet have an explanation for this relationship, and further research is needed.
[It would appear that some of our indicators are not measuring the same thing? Some seem consistent to each other, but do not heavily impact economic development benchmark. Another indicator is wildly correlated, but we haven’t a clue as to why?]
Table 2: Pearson Correlations of Indicators
|
Self Emp |
K. Index |
BDS |
SCI&ENG |
Patents |
VC/GSP |
R&D/GSP |
Inc |
GSP/cap |
|
| Self Emp |
1 |
0.338 |
0.040 |
0.317 |
0.274 |
0.072 |
0.998 |
-0.188 |
0.075 |
| Kauffman Index |
0.338 |
1 |
0.655 |
-0.274 |
0.157 |
0.136 |
0.397 |
0.039 |
-0.077 |
| BDS |
0.040 |
0.655 |
1 |
-0.338 |
0.150 |
0.112 |
0.083 |
0.384 |
0.014 |
| SCI&ENG |
0.317 |
-0.274 |
-0.338 |
1 |
0.420 |
0.443 |
0.291 |
0.238 |
0.125 |
| Patents |
0.274 |
0.157 |
0.150 |
0.420 |
1 |
0.399 |
0.279 |
0.152 |
0.062 |
| VC/GSP |
0.072 |
0.136 |
0.112 |
0.443 |
0.399 |
1 |
0.079 |
0.472 |
0.300 |
| R&D/GSP |
0.998 |
0.397 |
0.083 |
0.291 |
0.279 |
0.079 |
1 |
-0.181 |
0.070 |
| Inc |
-0.188 |
0.039 |
0.384 |
0.238 |
0.152 |
0.472 |
-0.181 |
1 |
0.221 |
| GSP/cap |
0.075 |
-0.077 |
0.014 |
0.125 |
0.062 |
0.300 |
0.070 |
0.221 |
1 |
In sum, this correlation analysis indicates that only a few selected indicators are correlated, and their correlation is only modest even within a single set of indicators. Between entrepreneurship and innovation, we find even less correlation between indicators. In other words, if you talk about entrepreneurship, the performance of each state can change substantially by selecting different indicators, and the same is true for innovation indicators.
It would appear that the indicators for both innovation and entrepreneurism, which seem ever so reasonable when we began this hypothetical endeavor, are just not related to each other. We of course do not mean to imply that these selected indicators are definitive concerning what is or is not appropriate to include as a measure of entrepreneurship or innovation. We simply would expect that someone looking to comprise an index of entrepreneurship and innovation might rely on these seemingly common sense measures. This correlation analysis leads us to suspect that any index, and its rankings, that use these common sense indicators will be very misleading at best, and quite possibly be just plain wrong. With the exception of self-employment and R&D, entrepreneurship and innovation indicators do not appear to have much correlation at the state level.
Simulation: Let’s Play Around and make our own state indexes.
Now we come to the most fun part of the exercise: to create your own state rankings. As we have demonstrated, our indicators for entrepreneurship and innovations, while lacking in statistical validity and correlating minimally with each other, could be used by anybody to construct their own state rankings and business climate index. By playing around with the indexes and the choice of which to use and how important each is in the statistical schema, you will more easily feel and actually see the subjectivity that can, without intention to manipulate, creep into almost any index and ranking system. Obviously, the reader should not actually intend to mislead someone with results from this exercise, but the creating of these rankings will demonstrate how little changes can affect rankings hugely. In this way, you can easily understand and demonstrate the subjectivity, or at least the volatility of these state rankings.
The first question to address in creating your own index, of course, is the criteria we will use to rank the states in a meaningful way. It turns out that there are hundreds of possibilities, many of which can be defended as logically sound and therefore assumed to have substantive results. We present several most logical methodologies here, in order to illustrate the diversity of real possibilities and the vastly different results we obtain from each of them. Perhaps the most straightforward methodology would be simply to order the states from 1 to 50 and score 50 to 1 along each of the indexes,[3] and then average all of the rankings. With this approach, Colorado comes out to be number 1.
Most rankings, however, weight their variables, under the assumption that some indicators are more important than others. We could argue that self-employment rates are highly important because they paint one of the broadest pictures of total entrepreneurial activity, and we seek to consider broad trends. Additionally, patents per Science & Engineering workforce may be seen as the closest measure of innovations in the indexes. We could argue that the Kauffman Index measure and Venture Capital measure are less significant than the others, as the Kauffman Index’s threshold for new entrepreneurial activity may be perceived as too low and because most firms do not receive venture capital financing.[4] If we weight the first two measures heavily, discount the last two, and maintain primarily even weights for the remaining measures, Oregon is number 1. 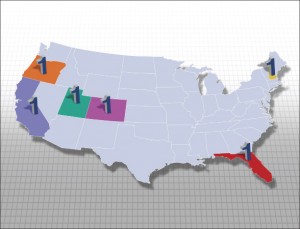
But on second thought, this doesn’t sound so correct. We should just drop the Venture Capital measure entirely, suggesting that VCs have limited interaction with most firms and, therefore, are not necessarily relevant to the large scope of entrepreneurship and innovation. The same could be said of science & engineering degree holders; some may believe that we should not overstate the importance of these specific degrees because everyone can be innovative in their own way. Furthermore, the BDS captures firms that employ at least one person besides the owner, and this could be seen as a more economically significant measure than self-employment. When we eliminate the Venture Capital and the Science & Engineering variables, and weight the BDS data more heavily, Florida is number 1.
We are not satisfied with this ranking either. It would be wrong to drop the VC and Science & Engineering degree holder measures. Instead, we should drop the Kauffman Index because of its threshold issue discussed previously. And although VCs and Science & Engineering degree holders are a minority of the population, some believe that they have an outsized impact on innovation and entrepreneurship, and should actually be weighted more heavily. The same people may suggest that the BDS should not be heavily weighted, but instead discounted because while employer firms are important, they can often be a lagging indicator of entrepreneurial activity. With this logic, it turns out that New Hampshire is number 1.
Thinking about this more though, this ranking seems unfair as well. We should not drop the Kauffman Index, because even though it is a low threshold for new entrepreneurial activity, it still captures a nice broad picture, just like self-employment. We could actually weight both of these heavily to again capture the broad effect. And real GSP per capita may be seen as the most accurate way to capture broad effects, so we could weight this heavily as well. It could be argued that patents are a poor proxy for innovations, so we should not consider this measure at all.[5] Last, the Inc. company measure is for fast-growing private firms only, and we know that firms of all sizes and statuses can be innovative and entrepreneurial, so we should not consider this measure either. Under this logic, it turns out that Montana is number 1.
Table 5: Top Five States for Four Scenarios
| Num |
1st Scenario |
2nd Scenario |
3rd Scenario |
4th Scenario |
| 1 | Oregon | Florida | New Hampshire | Montana |
| 2 | California | Colorado | Colorado | Colorado |
| 3 | Colorado | Idaho | California | Vermont |
| 4 | Vermont | California | Washington | California |
| 5 | New Hampshire | Utah | Massachusetts | Maine |
If we list the top five states under each scenario, we find that certain states, such as California and Colorado, often appear in the top five, but most other states are not consistently in the top five. The diversity of the findings is surprising, given that each scenario is an attempt to measure entrepreneurship and innovations. It is hard to believe that we are talking about the same thing. While the logic sounds reasonable in each case, the results are inconsistent. In our final exercise, we randomly weight each measure. Below we present the simulated results for 1000 scenarios. We randomly generated different weights, computed a final ranking, and then tabulated number one, top five, and top ten ranking appearances for each state.[6]
It appears as though we missed some opportunities to find Utah, California, and Vermont as number 1 in our individual weighting exercises. But Montana, Florida, or Oregon never randomly came out as number 1 in the random scenarios, and our logic above seems defendable in each individual case. It is also curious that a state like Vermont appears as number one sixteen times, and Utah only once, but Utah appears many more times in the Top Five and Top Ten counts. Similarly, Idaho appears in the Top Five many more times than New York, but this is reversed for the Top Ten count. Overall, in the randomized simulations, five states can become number 1, 16 states are eligible for the Top Five, and 22 states are eligible for the Top Ten. Interested state officials can contact us for the secret sauce of weights, but at the end of the day, it seems we cannot trust these random simulations either. Assigning weight is an art, and anyone can manipulate rankings.
Table 6: Simulation Result
|
State |
First Place Appearances |
Top Five Appearances |
Top Ten Appearances |
| Colorado |
749 |
1000 |
1000 |
| California |
227 |
999 |
1000 |
| Oregon |
0 |
743 |
999 |
| New Hampshire |
7 |
684 |
941 |
| Utah |
1 |
537 |
928 |
| New York |
0 |
65 |
803 |
| Washington |
0 |
207 |
795 |
| Massachusetts |
0 |
183 |
710 |
| Vermont |
16 |
291 |
656 |
| Idaho |
0 |
142 |
550 |
| Florida |
0 |
38 |
335 |
| Georgia |
0 |
32 |
320 |
| Montana |
0 |
62 |
276 |
| Arizona |
0 |
8 |
246 |
| Minnesota |
0 |
0 |
208 |
| Maine |
0 |
2 |
112 |
| Connecticut |
0 |
0 |
41 |
| Texas |
0 |
3 |
39 |
| Maryland |
0 |
0 |
30 |
| South Dakota |
0 |
0 |
1 |
| Iowa |
0 |
0 |
1 |
| Virginia |
0 |
0 |
1 |
Conclusions and Implications
State rankings of economic performance measures are popular among think tanks, policymakers, media, and even some academics, but the connection between these indexes and actual economic growth and performance has been found to be ambiguous. In this paper, we focused specifically on measures of entrepreneurship and innovation. A series of tests with three measures of entrepreneurial activity and five measures of innovative activity resulted in minimal or modest correlation between most measures, contrary to what we would expect. This finding is confirmed by bivariate analysis with Pearson correlations and multivariate analysis with principal component analysis.
We then allowed the reader to see how different rankings of states could be generated with the eight measures to show that variations in weighting–frequently used by popular indexes–and different compositions of the eight measures can drastically affect the results. Indeed, as a random weighting simulation reveals, many states are “eligible” for high rankings. That is, the process of selecting and weighting indicators seems more like an art than a science. How, then, should states respond to popular ranking exercises? The principle objective of data collection is that data is a tool to inform us about the current state and the limitations of a jurisdiction. It is not the end to determine meaning or to provide politically-motivated justification.
We thus offer four primary recommendations. 
First, policymakers should not rely on a single indicator to gauge economic conditions. We have demonstrated that the variability of indicators even within a single concept, say entrepreneurship, means there is a multi-dimensionality of measurement at the state level. We have to be cautious about the meaning of each indicator, as well as its limitations.
Second, aggregating indicators also does not provide solutions, again due to the variability of indicators. Aggregating indicators may provide nuance, but the nuance has to be interpreted cautiously. In addition to the indicators we have discussed, we could add more indicators, such as the number of small businesses for entrepreneurship and the amount of federal research funding, e.g., Small Business Innovation Research grants, for innovation. But readers can easily guess by now that adding more indicators, and creating a ranking using them does not necessarily mean the rankings become more comprehensive or objective. We simply have to avoid a normative approach here; more indicators do not result in a better ranking.
Third, as these rankings are not meaningful, policymakers should not see improving their rankings as an objective. And along the same lines, rankings should not be used as a justification for action or achievement.
And fourth, we suggest a scorecard approach as a more meaningful measure than a ranking. Ranking, by definition, is a uni-dimensional measure, and argues that State X is better than State Y. A scorecard decomposes and reveals the areas in which each state has strengths and weaknesses. This approach is not only more meaningful, but also it may open up a healthier discussion about potential improvements. For instance, thumbtack.com’s Small Business Friendliness Survey presents business owners’ perceptions of their regulatory environment in six different areas: health, labor, tax code, licensing, environment, and zoning. While aggregating these scores to assess the overall regulatory environment would not be terribly productive, the scorecard provides a clearer message to each state about the regulatory areas in which they do well and those in which they need to improve.
ADDENDUM: BUSINESS CLIMATE INDEX “FLEXIBILITY” USING EVEN MORE ADVANCED STATISTICAL METHODOLOGY: PRINCIPAL COMPONENT ANALYSIS
To further demonstrate the weakness of our indicators for innovation and entrepreneurism, we have subjected them to analysis by principal component analysis. Principal Component Analysis can be used to investigate connections between several indicators (i.e., multivariate) interacting at the same time.
[READER: Stick with me now–There are two conventional ways to decipher the results of principal component analysis. The first is to see how many principal components it takes to amass a cumulative total exceeding 0.9–which means we can “account for” ninety per cent of the explanation with these principal components. If it takes a lot of principal components to reach the .09 that means each of the components are not really explaining very much and in this case the more the merrier is not good. The second criterion is to evaluate a principal component to see if the principal component has a standard deviation (an eigenvalue to the geeks) of 1 or more. Trust me, you don’t want an explanation of this one–just go with a standard deviation of one or more (see comment 1 below).
With the first approach, we need to count at least five PCs to get the cumulative portion of more than 90 percent (See Table 3) [this is not good]. If we do so, it means that those five PCs can explain 94.5 percent of the variation with the indicators. This is something, but not very helpful because we have to have five PCs out of eight indicators. A principal component analysis with a total of eight indicators would be most useful if we could extract one or two, or perhaps a maximum of three components.[2]
Table 3: Results of Principal Component Analysis
|
PC1 |
PC2 |
PC3 |
PC4 |
PC5 |
PC6 |
PC7 |
PC8 |
|
| Standard deviation |
1.621 |
1.374 |
1.364 |
0.824 |
0.710 |
0.504 |
0.432 |
0.003 |
| Proportion of Variance |
0.329 |
0.236 |
0.233 |
0.085 |
0.063 |
0.032 |
0.023 |
0.000 |
| Cumulative Proportion |
0.329 |
0.565 |
0.797 |
0.882 |
0.945 |
0.977 |
1.000 |
1.000 |
The second approach reveals that there are three PCs that have a standard deviation greater than 1.0 (PC3 = 1.364). The first PC is composed of self-employment and R&D (See Table 4). We saw this odd combination in the correlation analysis, and the high correlation does not make sense to us conceptually, nor is the meaning of their combination clear. Thus, we cannot establish the meaning of this PC. The second PC is composed of Science & Engineering, Venture Capital, and some negative factor of the Kauffman Index. Again, it is hard to interpret the significance of this PC. The third PC is composed of negative factors of BDS and Inc. Most Inc. companies are relatively young, with a mean age of seven to eight years (Motoyama and Danley, 2012), but they have to be at least four years old to be included in the list. That is, the Inc. indicator does not overlap much with BDS data, which captures firms that are five years old or younger. The meaning of this PC, then, is also difficult to interpret.
Table 4: Rotated Matrix of PCs
|
PC1 |
PC2 |
PC3 |
PC4 |
PC5 |
PC6 |
PC7 |
PC8 |
|
| Self Employment |
0.515 |
-0.168 |
0.324 |
0.229 |
0.090 |
0.234 |
0.002 |
0.697 |
| Kauffman Index |
0.324 |
-0.450 |
-0.304 |
-0.074 |
-0.333 |
-0.564 |
0.405 |
0.049 |
| BDS |
0.186 |
-0.338 |
-0.551 |
-0.008 |
0.287 |
0.015 |
-0.682 |
-0.001 |
| Science & Engineer |
0.291 |
0.545 |
0.183 |
0.128 |
0.141 |
-0.679 |
-0.296 |
0.000 |
| Patents |
0.379 |
0.244 |
-0.097 |
-0.807 |
0.277 |
0.154 |
0.190 |
0.001 |
| Venture Capital |
0.288 |
0.405 |
-0.305 |
0.059 |
-0.731 |
0.303 |
-0.178 |
0.000 |
| R&D |
0.524 |
-0.194 |
0.296 |
0.217 |
0.064 |
0.190 |
0.030 |
-0.715 |
| Inc. 500 |
0.095 |
0.312 |
-0.526 |
0.473 |
0.404 |
0.121 |
0.464 |
-0.001 |
These findings suggest that the multivariate statistical procedure of principal component analysis does not help us to extract useful PCs or combinations of indicators, either. It simply means that even within the theme of entrepreneurship and innovation, the variation of indicators is so large and unconnected that there is no small set of representative indicators.
Comment 1: Statisticians, such as Marriott (1974), caution against this approach, and we will avoid any over-simplification or over-interpretation.
Footnotes
[1] We follow the method by Everitt and Hothorn (2011). We clarify that we have a sample of more than 50, the minimum number suggested by Guadagnoli and Velicer (1988). Also, the ratio between the sample and variables is larger than five, as suggested by Gorsuch (1983) and Hatcher (1994).
[2] There are indeed cases (e.g., Olympic heptathlon results) in which a small number of PCs can explain the most variation.
[3] This is just one of many ways to create rankings. If you create a ranking based on the raw ratio, it will be even easier to manipulate the result, given skewed distribution of most variables. Here, we have no intention to argue which method is better, but to demonstrate that a simpler and easier method can still lead to substantially manipulated rankings.
[4] See Fairlie (2013) for a technical discussion of the Kauffman Index. The threshold for defining new entrepreneurial activity stems from new business owners working fifteen hours or more per week on their businesses as their main jobs. For the purposes of scenarios 2 and 3 we argue this is too low of a threshold for a measure of new entrepreneurial activity, and for the purposes of scenarios 1 and 4 that it is not a problem.
[5] Patents are only one way to measure innovation. Not all innovations are patentable, as evidenced by the significant variance in patenting intensity by industry (U.S. Department of Commerce 2012). While we would expect certain industries could be more or less ‘innovative’ than others, the large variances in patenting activity suggest patents undercount innovations in some industries. Moreover, academics have long concerned themselves about whether the measurement of patents citations is an appropriate measure of innovation and knowledge flows. See Roach and Cohen (2012) for a discussion. This has generated debate amongst those who rely and those who don’t rely on patent measures, and we play both sides of the debate for the purpose of our simulation. For scenario 4, we agree that they are a poor measure; for all others we agree they are fine.
[6] For top five and top ten simulations, ties extending beyond 5th and 10th place respectively are dropped.
References
Chapple, Karen, Ann Markusen, Greg Schrock, Daisaku Yamamoto, and Pingkang Yu. 2004. “Gauging metropolitan “high-tech” and “I-tech” activity.” Economic Development Quarterly no. 18 (1):10-29.
Cortright, Joseph, and Heike Mayer. 2004. “Increasingly rank: The use and misuse of rankings in economic development.” Economic Development Quarterly no. 18 (1):34-39.
Everitt, Brian, and Torsten Hothorn. 2011. An introduction to applied multivariate analysis with R. London: Springer.
Fairlie, Robert W. 2013. “Kauffman Index of Entrepreneurial Activity 1996-2012.” Kansas City, MO: Kauffman Foundation. Fisher, Peter. 2005. Grading places: What do the business climate rankings really tell us? Washington DC: Economic Policy Institute.
Gorsuch, Richard L. 1983. Factor analysis. HIllsdale, NJ: Lawrence Erlbaum Associates.
Gottlieb, Paul D. 2004. “Response: Different purposes, different measures.” Economic Development Quarterly no. 18 (1):40-43.
Guadagnoli, Edward, and Wayne F. Velicer. 1988. “Relation of sample size to the stability of compnent patterns.” Psychological Bulletin no. 103 (2):265-275.
Hatcher, Larry. 1994. A step-by-step approach to using the SAS system for factor analysis and strucutral equation modeling. Cary, NC: SAS Institute.
Kolko, Jed, David Newmark, and Marisol Cuellar Mejia. 2011. Public policy, state business climates, and economic growth. In NBER Working Paper. Cambridge, MA: National Bureau of Economic Research.
Mariott, Francis H.C. 1974. The interpretation of multiple observations. London: Academic Press.
Motoyama, Yasuyuki, and Brian Danley. 2012. The ascent of America’s high-growth companies: An analysis of the geography of entrepreneurship. In Kauffman Research Paper Series. Kansas City, MO: Kauffman Foundation.
Motoyama, Yasuyuki, and Iris Hui. 2014. “How do business owners perceive the state business climate? Using hierarchical models to examine business climate perception and state rankings.” Economic Development Quarterly.
Pacific Research Institute. 2008. Economic Freedom Index. edited by Lawrence J. McQuillan, Michael T. Maloney, Eric Daniels and Brent M. Eastwood. San Francisco: PRI.
Plaut, Thomas R., and Joseph E. Pluta. 1983. “Business climate, taxes and expenditures and state industrial growth in the United States.” Southern Economic Journal no. 50 (1):99-119.
Roach, Michael, and Wesley M. Cohen. 2012. “Lens or Prism? Patent Citations as a Measure of Knowledge Flows from Public Research.” Management Science.
Forthcoming. Schumpeter, Joseph Alois. 1912. Theorie der wirtschaftlichen entwicklung (Theory of Economic Development). Leipzig,: Duncker & Humblot.
Skoro, Charles L. 1988. “Rankings of state business climates: An evaluation fo their usefulness in forecasting.” Economic Development Quarterly no. 2 (2):138-152. Small Business and Entrepreneurship Council (SBEC). 2011.
Small Business Survival Index: Ranking the Policy Environment for Entrepreneurship Across the Nation. edited by Raymond J. Keating. Washington DC: SBEC.
Steinnes, Donald N. 1984. “Business climate, tax incentives, and regional economic development.” Growth and Change no. 15 (2):38-47.
U.S. Department of Commerce. 2012. Economics and Statistics Administration. United States Patent and Trademark Office. Intellectual Property and the U.S. Economy: Industries in Focus.


Comments
Hi, this really is such a great topic to read about.
Comment by vidasaludablehoy.weebly.com on February 17, 2014 at 12:49 am
Trackbacks
The comments are closed.